Visualizing Uncertainty

Claus O. Wilke

2025-06-22

We all know how to visualize uncertainty, right?

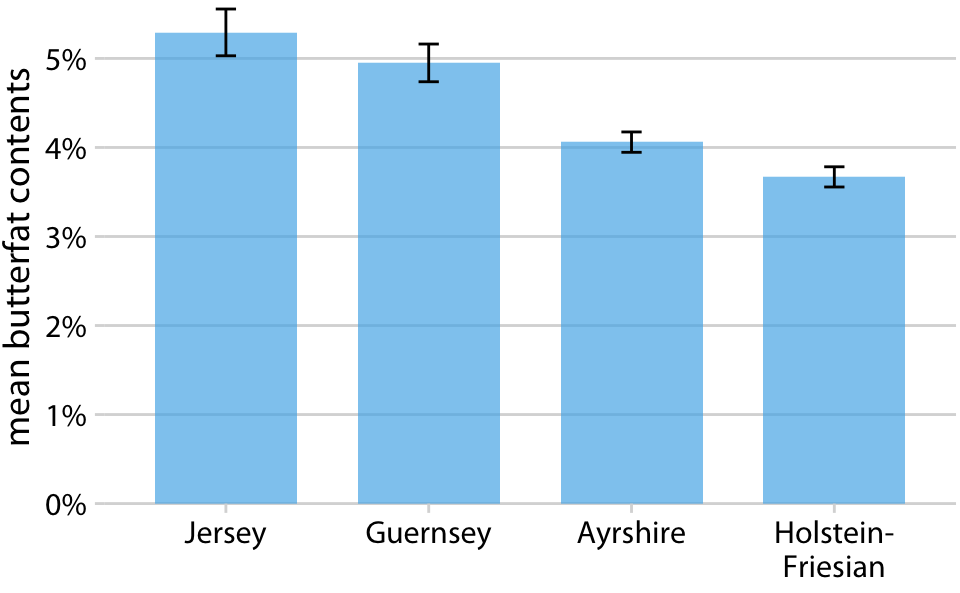
Milk butterfat contents by cattle breed. Source: Canadian Record of Performance for Purebred Dairy Cattle

We all know how to visualize uncertainty, right?

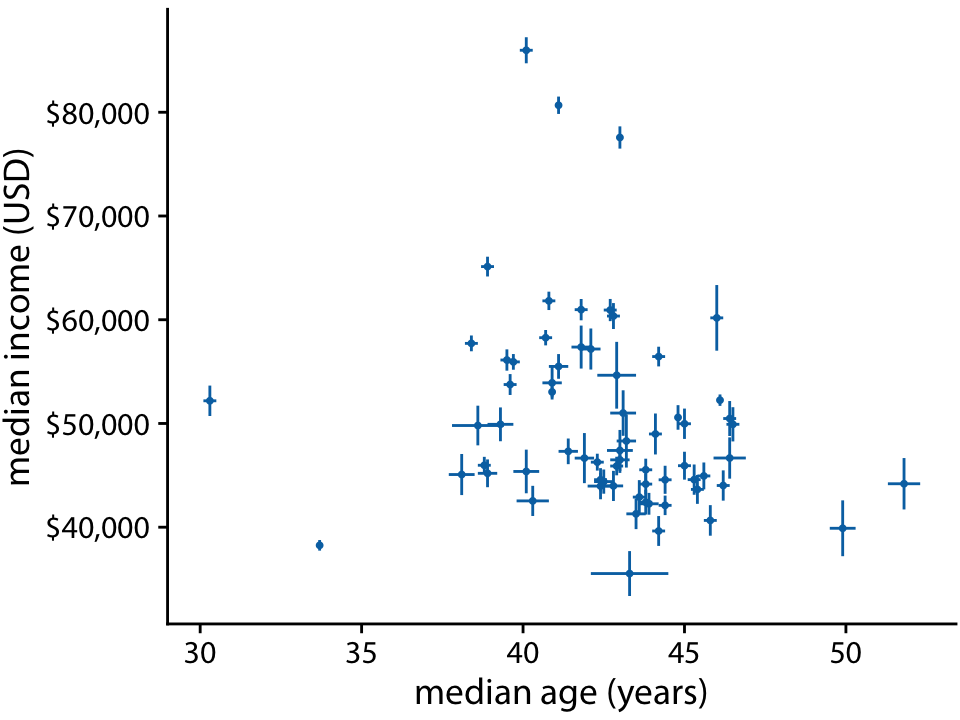
Income versus age for 67 counties in Pennsylvania. Source: 2015 Five-Year American Community Survey

We all know how to visualize uncertainty, right?

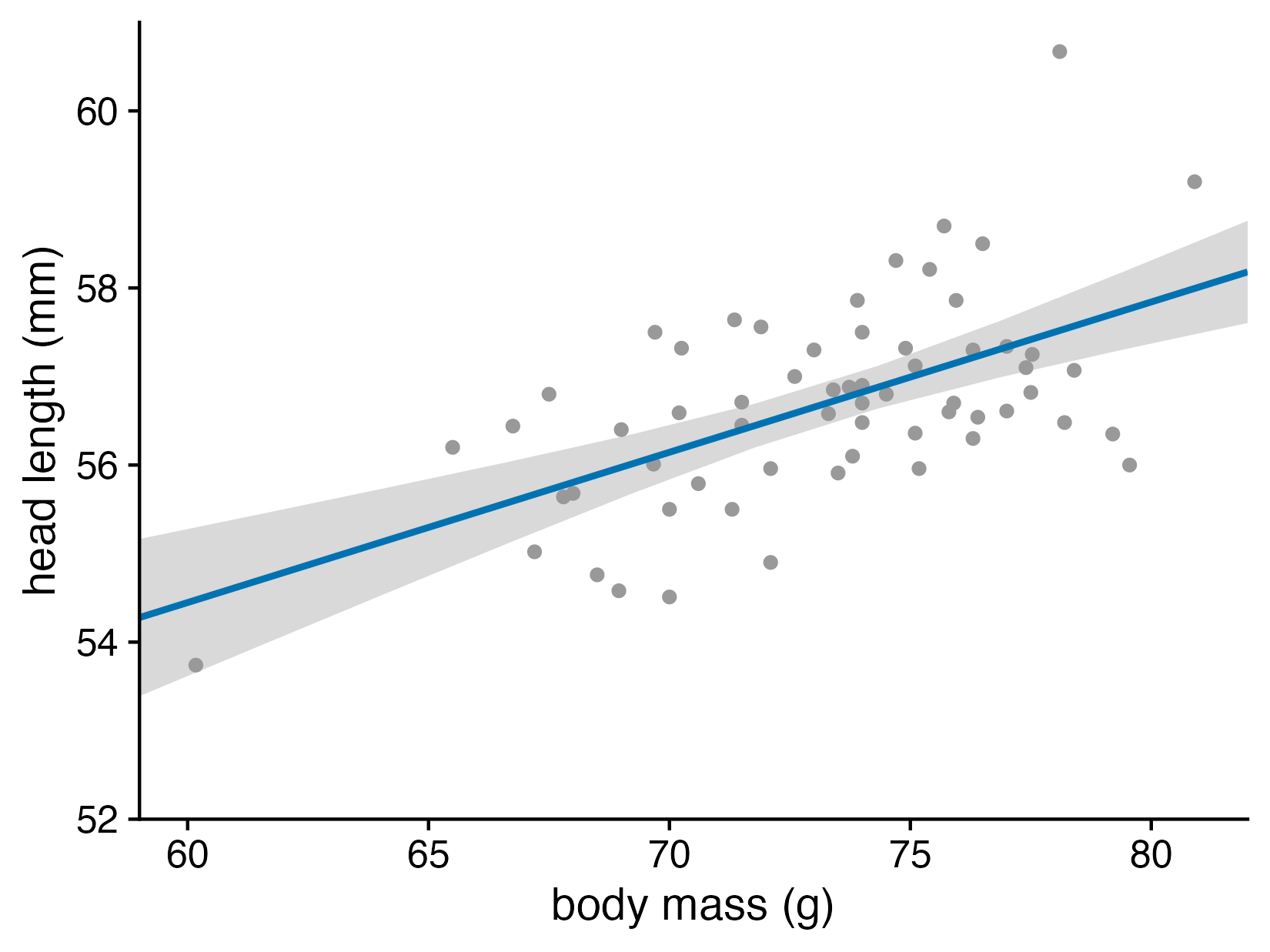
Head length versus body mass for male blue jays. Data source: Keith Tarvin, Oberlin College

These commonly used visualizations have problems

  • It’s often not clear what exactly the visualizations represent
  • Even if we know, we can have difficulty interpreting what we see

It’s often not clear what the visualizations represent

In particular, error bars can represent many different quantities

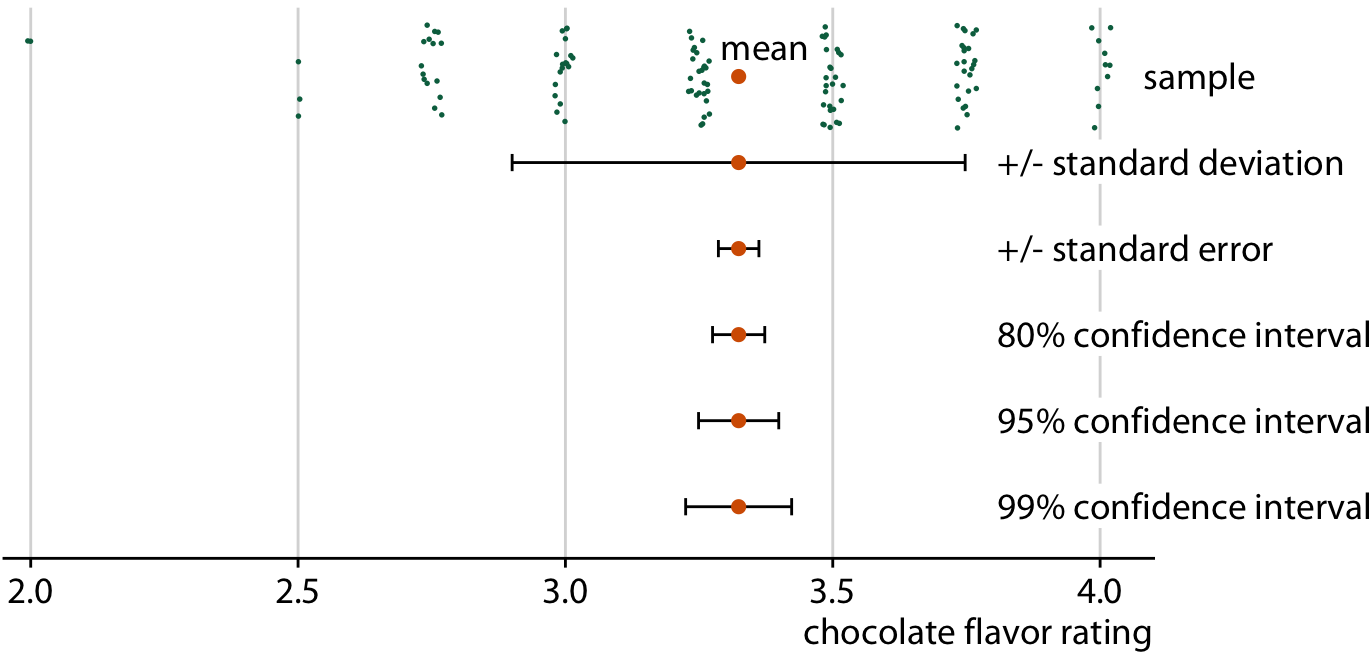
Chocolate bar ratings. Source: Manhattan Chocolate Society

We can have difficulty interpreting what we see

  • People are not good at reasoning about probabilities
  • People will substitute uncertainty with simpler concepts
    (Deterministic Construal Error)
  • People will interpret intervals as hard boundaries

Lace Padilla, Matthew Kay, and Jessica Hullman (2022): Uncertainty Visualization

Uncertainty shown as 95% CI error bars with caps

Chocolate bars from four countries compared to bars from the US
 

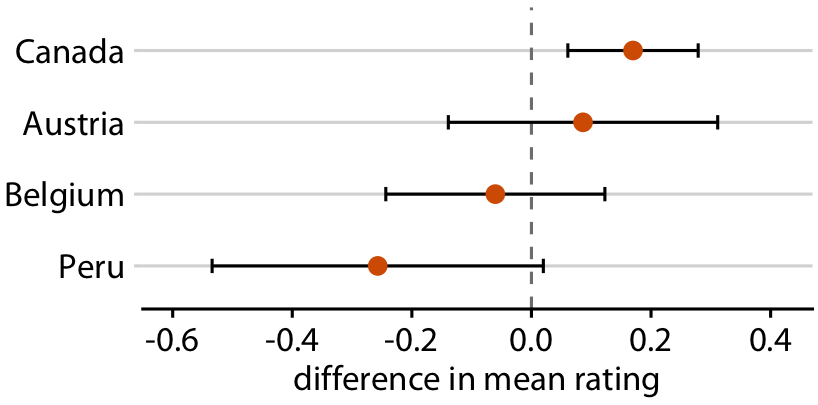
Relative rankings compared to US chocolate bars. Source: Manhattan Chocolate Society

Uncertainty shown as 95% CI error bars with caps

Determinstic Construal Error:
Error bars are interpreted as min/max values

Relative rankings compared to US chocolate bars. Source: Manhattan Chocolate Society

Uncertainty shown as 95% CI error bars with caps

Categorical thinking:
Areas outside and inside the error bars are categorically different

Relative rankings compared to US chocolate bars. Source: Manhattan Chocolate Society

Uncertainty shown as 95% CI error bars without caps

You can remove caps to make the boundary visually less severe
 

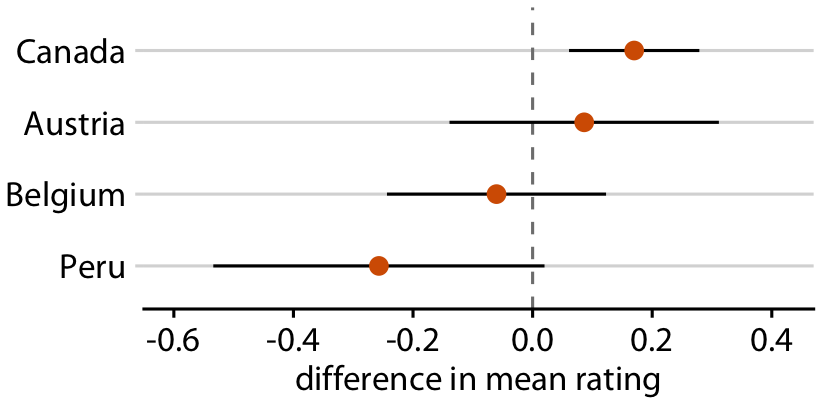
Relative rankings compared to US chocolate bars. Source: Manhattan Chocolate Society

Uncertainty shown as graded error bars

You can show multiple confidence levels to de-emphasize existence of boundary

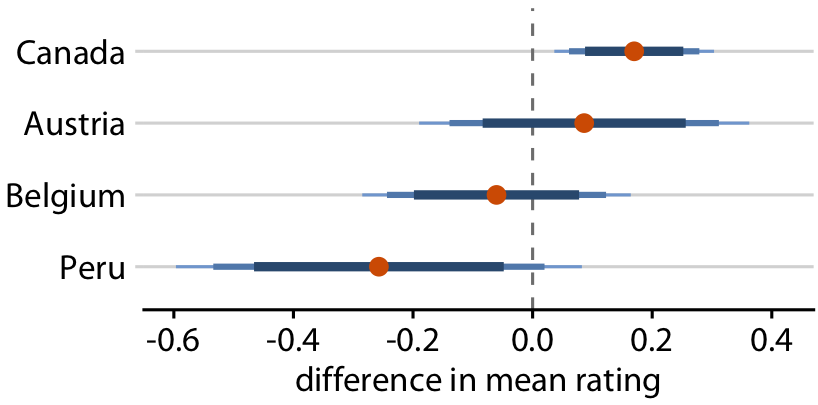
Relative rankings compared to US chocolate bars. Source: Manhattan Chocolate Society

Uncertainty shown as confidence strips

You can use faded strips (but hard to read/interpret)
 

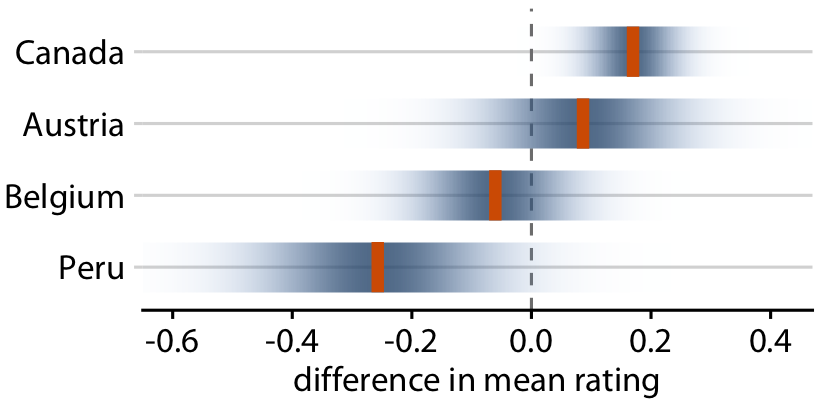
Relative rankings compared to US chocolate bars. Source: Manhattan Chocolate Society

Uncertainty shown as distributions

You can show actual distributions
Popular in Bayesian inference, but still difficult to interpret

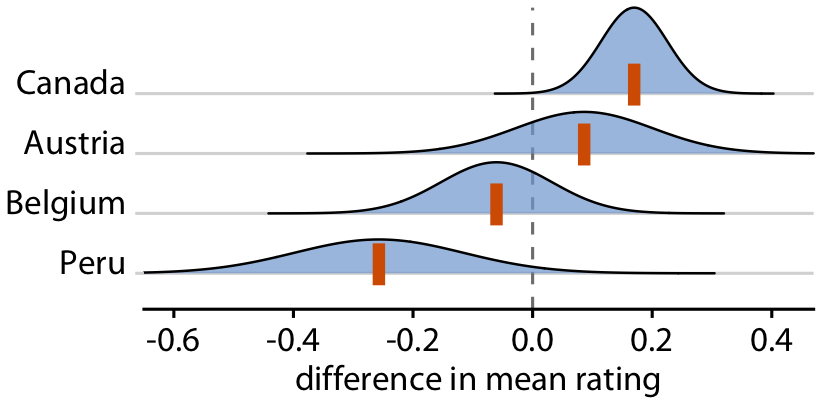
Relative rankings compared to US chocolate bars. Source: Manhattan Chocolate Society

Consider the actual experience of a customer

If I can buy either a Canadian or a US bar, what is the probability that the Canadian bar will be better?

Answer: The Canadian bar has a 53% chance of being better

How can we communicate this?

Use frequency framing to communicate probabilities

 

Use frequency framing to communicate probabilities

 

Use frequency framing to communicate probabilities

 

Use frequency framing to communicate probabilities

 

Use frequency framing to communicate probabilities

 

Alternatively: Use Hypothetical Outcome Plots

Hypothetical Outcome Plots use animation to let viewers experience uncertainty

Hullman et al., PLOS ONE 2015

Alternatively: Use Hypothetical Outcome Plots

Hypothetical Outcome Plots use animation to let viewers experience uncertainty

Hullman et al., PLOS ONE 2015

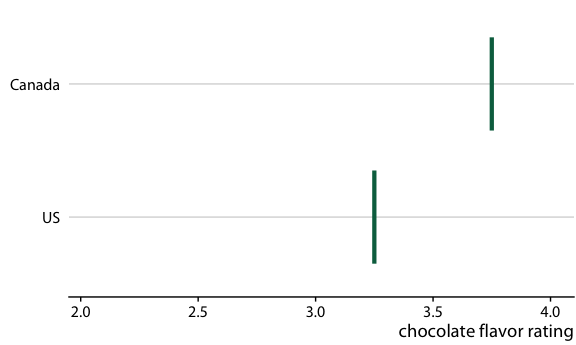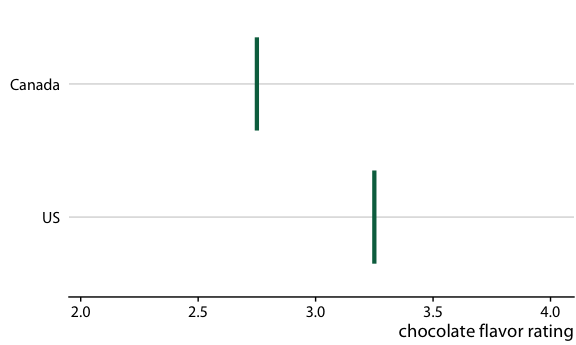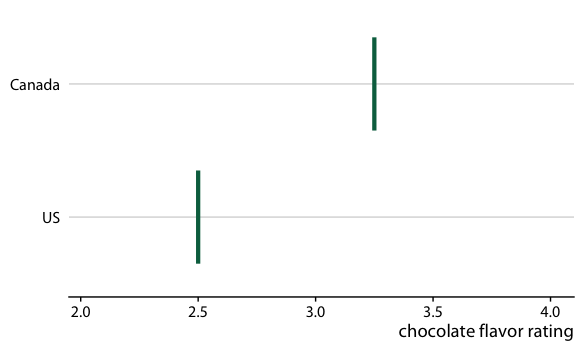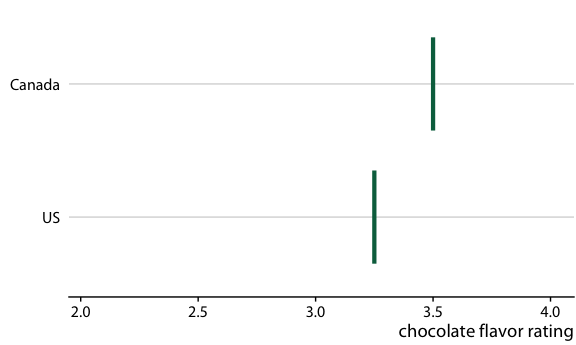
Uncertainty of trend lines

Let’s now consider the uncertainty of trend lines

What does the confidence band show?

Head length versus body mass for male blue jays. Data source: Keith Tarvin, Oberlin College

Let’s now consider the uncertainty of trend lines

Both the intercept and the slope have uncertainty

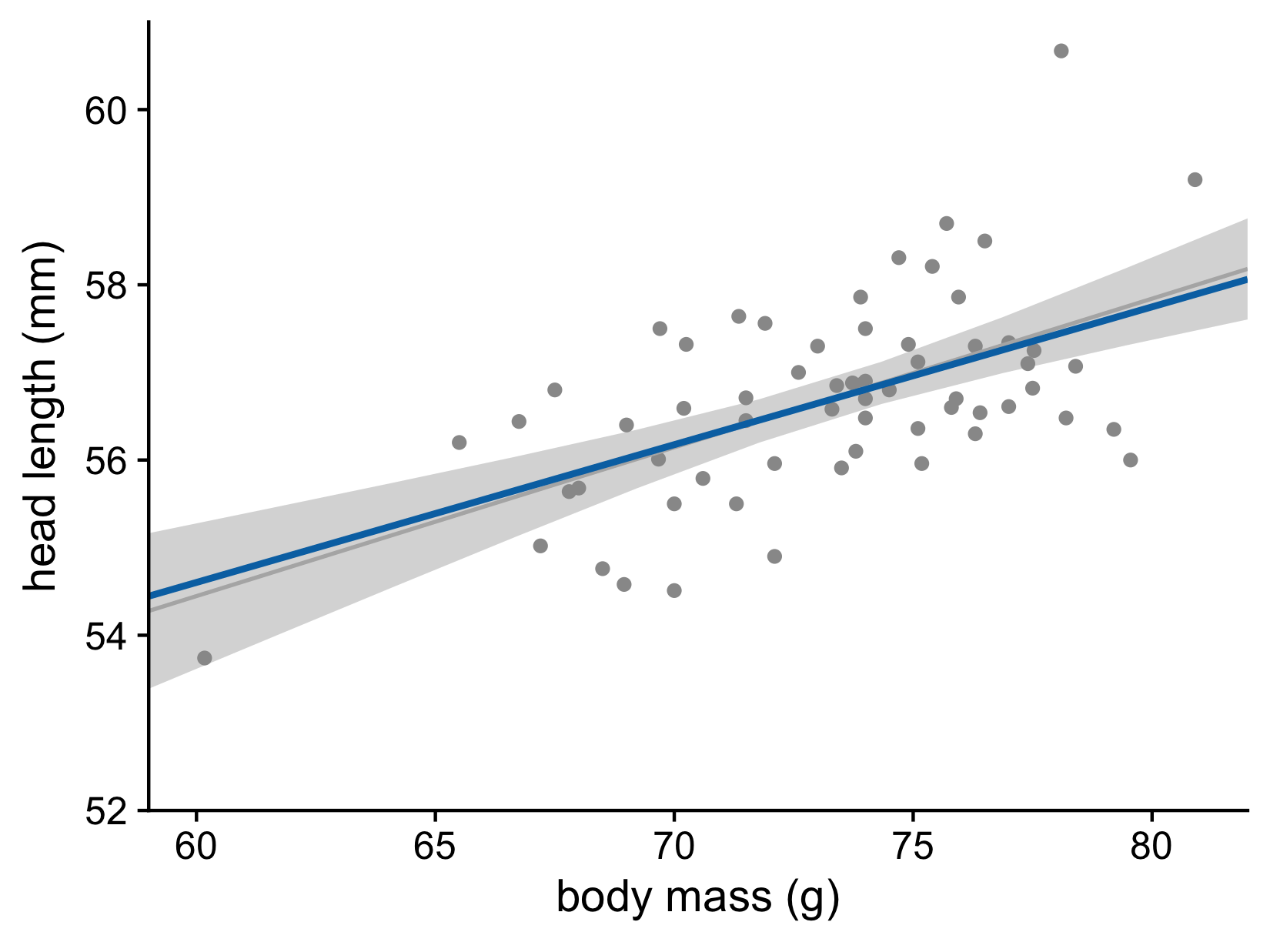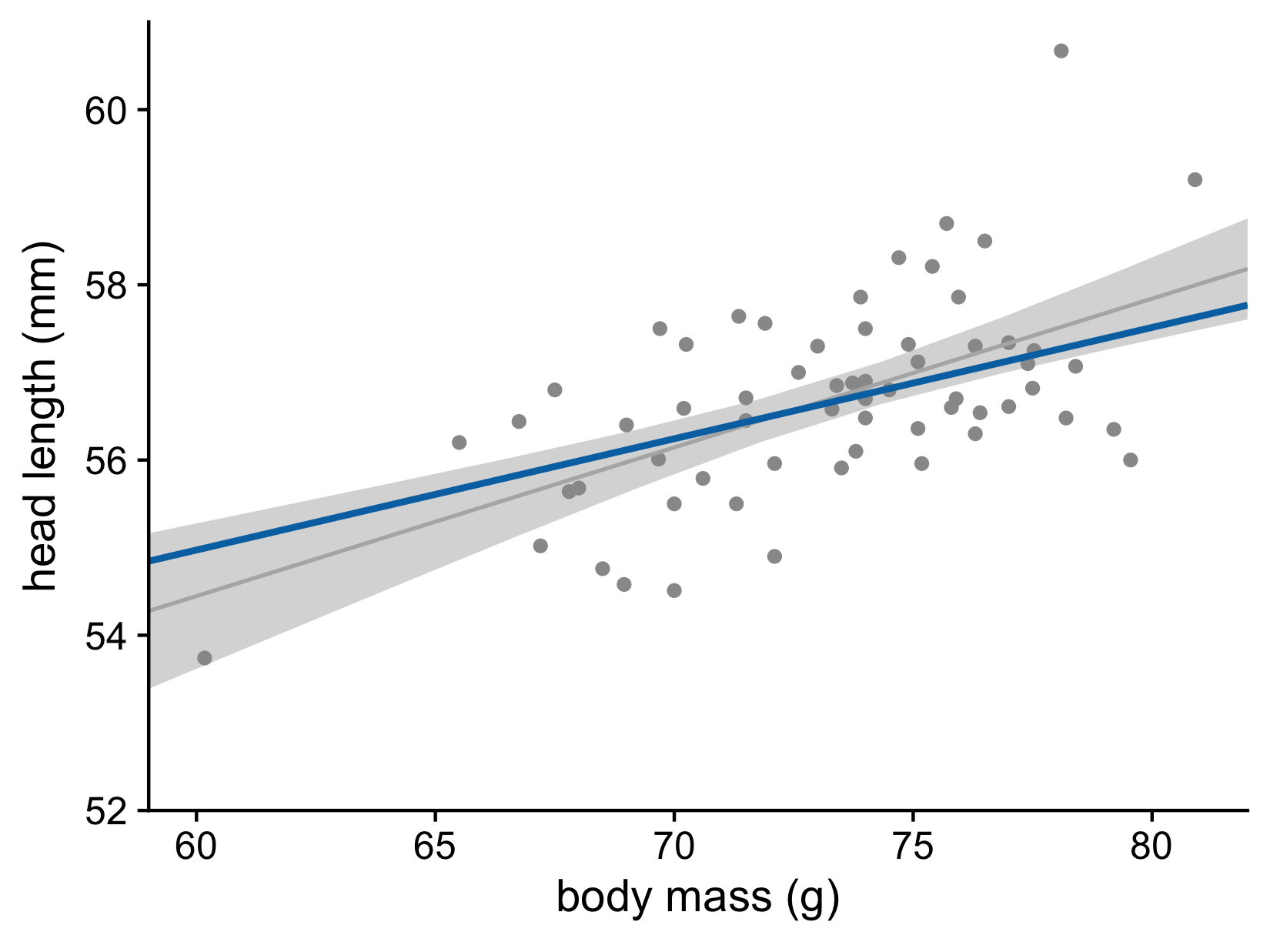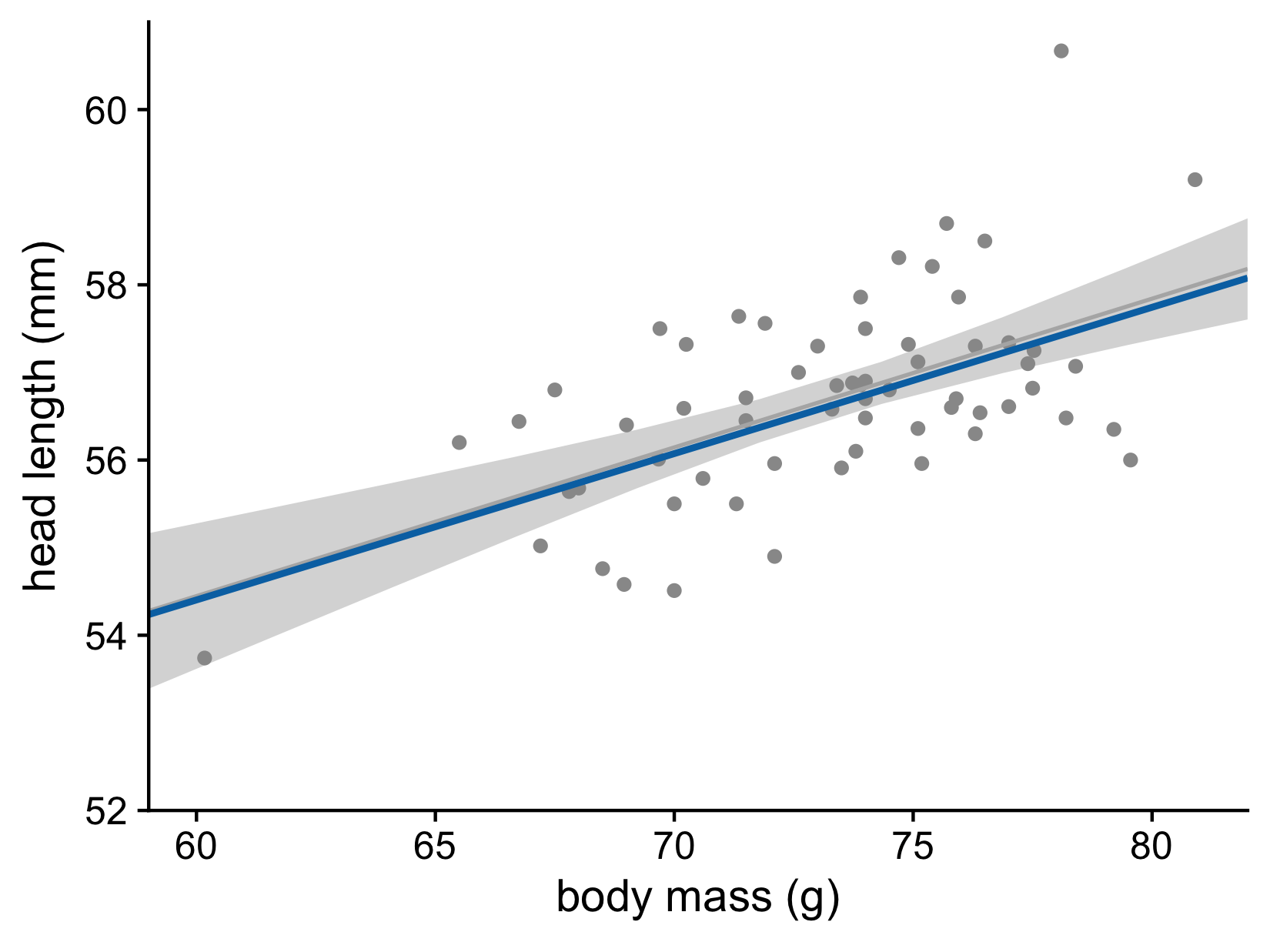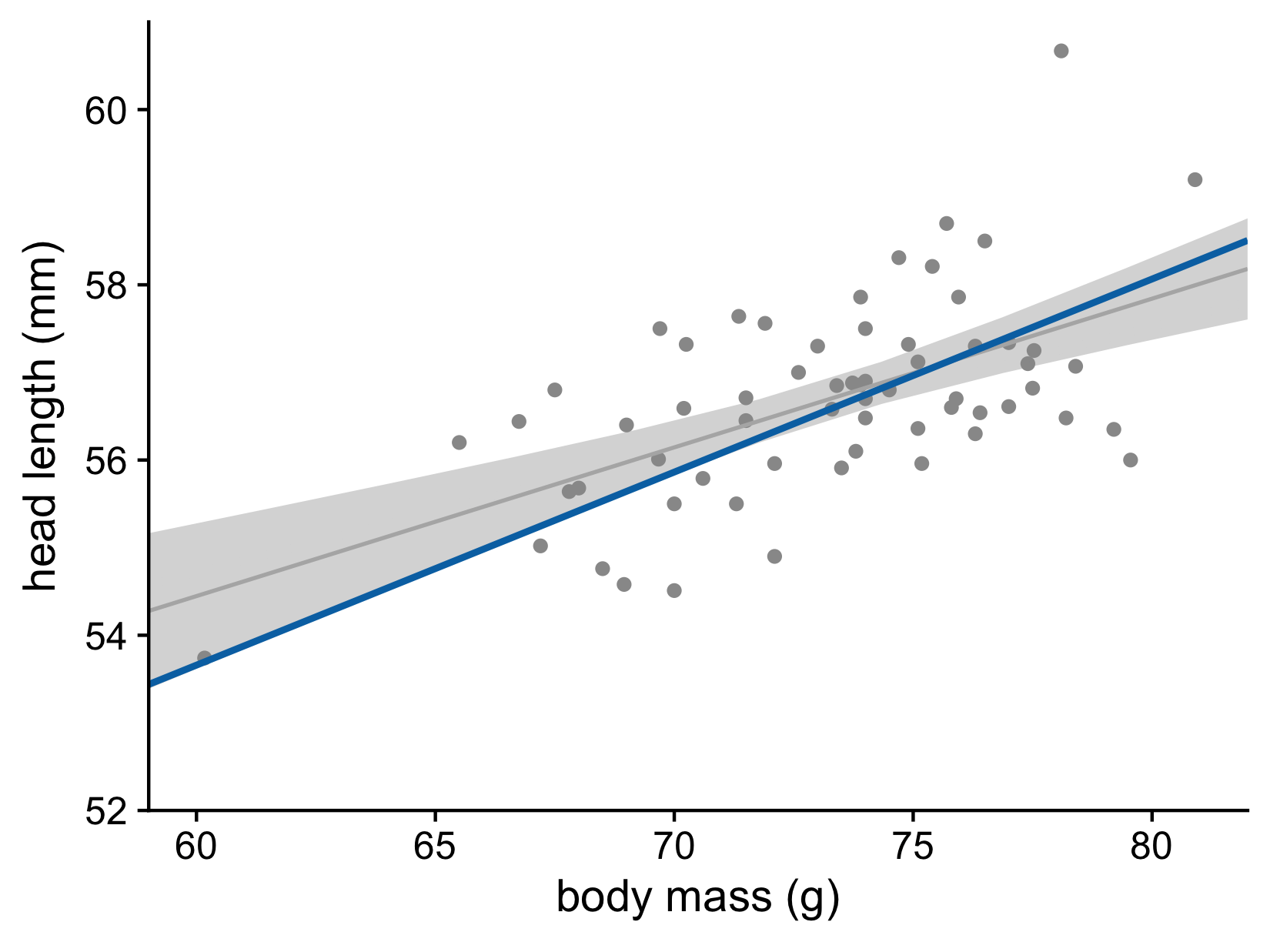
Head length versus body mass for male blue jays. Data source: Keith Tarvin, Oberlin College

It gets even more confusing for non-linear trend lines

Individual sample fits tend to be more wiggly than the mean

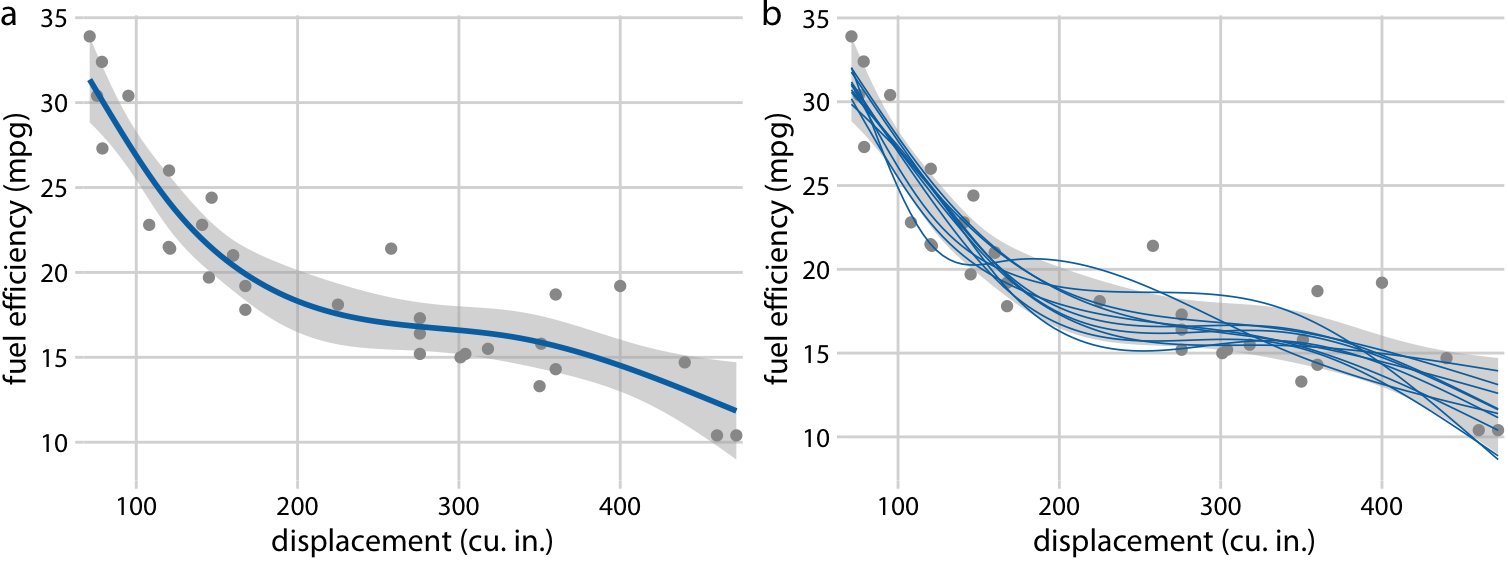
Fuel efficiency versus displacement, for 32 cars (1973–74 models). Source: Motor Trend, 1974

Hypothetical Outcome Plots again help develop intuition

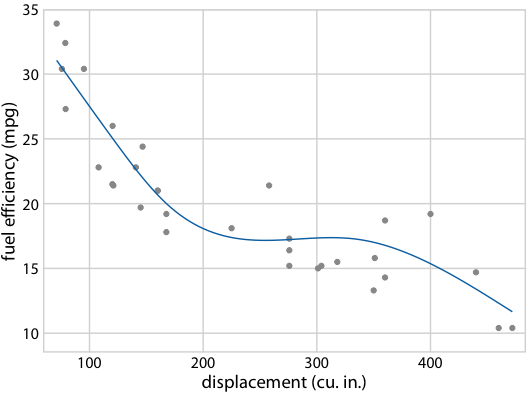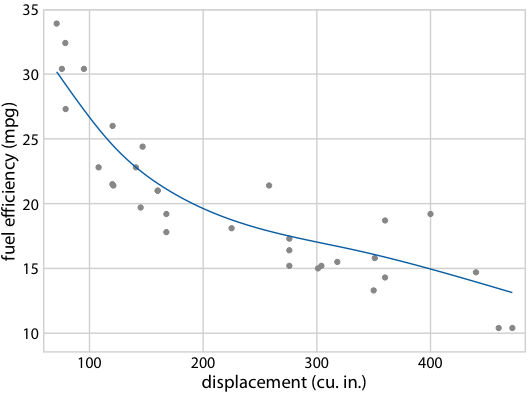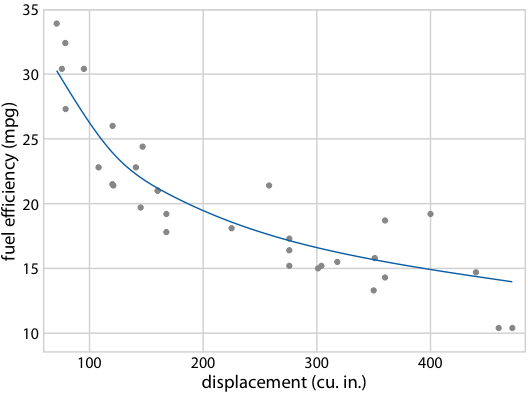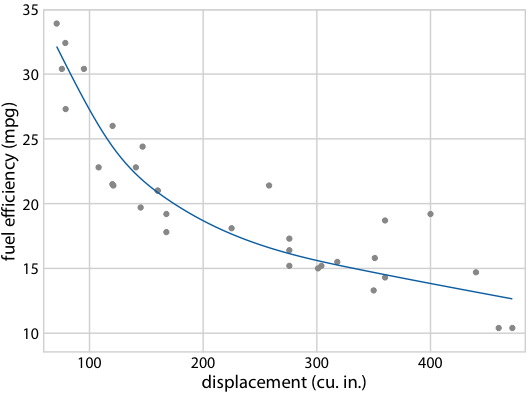
Fuel efficiency versus displacement, for 32 cars (1973–74 models). Source: Motor Trend, 1974

Uncertainty visualizations in R

Getting the data

The gapminder dataset:

library(gapminder)

gapminder
# A tibble: 1,704 × 6
   country     continent  year lifeExp      pop gdpPercap
   <fct>       <fct>     <int>   <dbl>    <int>     <dbl>
 1 Afghanistan Asia       1952    28.8  8425333      779.
 2 Afghanistan Asia       1957    30.3  9240934      821.
 3 Afghanistan Asia       1962    32.0 10267083      853.
 4 Afghanistan Asia       1967    34.0 11537966      836.
 5 Afghanistan Asia       1972    36.1 13079460      740.
 6 Afghanistan Asia       1977    38.4 14880372      786.
 7 Afghanistan Asia       1982    39.9 12881816      978.
 8 Afghanistan Asia       1987    40.8 13867957      852.
 9 Afghanistan Asia       1992    41.7 16317921      649.
10 Afghanistan Asia       1997    41.8 22227415      635.
# ℹ 1,694 more rows

Making a plot with error bars

Example: Relationship between life expectancy and GDP per capita

 

Making a plot with error bars

Example: Relationship between life expectancy and GDP per capita

 

 

Making a plot with error bars

lm_data <- gapminder |>
  nest(data = -c(continent, year))

lm_data
# A tibble: 60 × 3
   continent  year data             
   <fct>     <int> <list>           
 1 Asia       1952 <tibble [33 × 4]>
 2 Asia       1957 <tibble [33 × 4]>
 3 Asia       1962 <tibble [33 × 4]>
 4 Asia       1967 <tibble [33 × 4]>
 5 Asia       1972 <tibble [33 × 4]>
 6 Asia       1977 <tibble [33 × 4]>
 7 Asia       1982 <tibble [33 × 4]>
 8 Asia       1987 <tibble [33 × 4]>
 9 Asia       1992 <tibble [33 × 4]>
10 Asia       1997 <tibble [33 × 4]>
# ℹ 50 more rows

Making a plot with error bars

lm_data <- gapminder |>
  nest(data = -c(continent, year)) |>
  mutate(
    fit = map(data, ~lm(lifeExp ~ log(gdpPercap), data = .x))
  )

lm_data
# A tibble: 60 × 4
   continent  year data              fit   
   <fct>     <int> <list>            <list>
 1 Asia       1952 <tibble [33 × 4]> <lm>  
 2 Asia       1957 <tibble [33 × 4]> <lm>  
 3 Asia       1962 <tibble [33 × 4]> <lm>  
 4 Asia       1967 <tibble [33 × 4]> <lm>  
 5 Asia       1972 <tibble [33 × 4]> <lm>  
 6 Asia       1977 <tibble [33 × 4]> <lm>  
 7 Asia       1982 <tibble [33 × 4]> <lm>  
 8 Asia       1987 <tibble [33 × 4]> <lm>  
 9 Asia       1992 <tibble [33 × 4]> <lm>  
10 Asia       1997 <tibble [33 × 4]> <lm>  
# ℹ 50 more rows

Making a plot with error bars

lm_data <- gapminder |>
  nest(data = -c(continent, year)) |>
  mutate(
    fit = map(data, ~lm(lifeExp ~ log(gdpPercap), data = .x)),
    tidy_out = map(fit, tidy)
  )

lm_data
# A tibble: 60 × 5
   continent  year data              fit    tidy_out        
   <fct>     <int> <list>            <list> <list>          
 1 Asia       1952 <tibble [33 × 4]> <lm>   <tibble [2 × 5]>
 2 Asia       1957 <tibble [33 × 4]> <lm>   <tibble [2 × 5]>
 3 Asia       1962 <tibble [33 × 4]> <lm>   <tibble [2 × 5]>
 4 Asia       1967 <tibble [33 × 4]> <lm>   <tibble [2 × 5]>
 5 Asia       1972 <tibble [33 × 4]> <lm>   <tibble [2 × 5]>
 6 Asia       1977 <tibble [33 × 4]> <lm>   <tibble [2 × 5]>
 7 Asia       1982 <tibble [33 × 4]> <lm>   <tibble [2 × 5]>
 8 Asia       1987 <tibble [33 × 4]> <lm>   <tibble [2 × 5]>
 9 Asia       1992 <tibble [33 × 4]> <lm>   <tibble [2 × 5]>
10 Asia       1997 <tibble [33 × 4]> <lm>   <tibble [2 × 5]>
# ℹ 50 more rows

Making a plot with error bars

lm_data <- gapminder |>
  nest(data = -c(continent, year)) |>
  mutate(
    fit = map(data, ~lm(lifeExp ~ log(gdpPercap), data = .x)),
    tidy_out = map(fit, tidy)
  ) |>
  unnest(cols = tidy_out)

lm_data
# A tibble: 120 × 9
   continent  year data     fit    term     estimate std.error statistic p.value
   <fct>     <int> <list>   <list> <chr>       <dbl>     <dbl>     <dbl>   <dbl>
 1 Asia       1952 <tibble> <lm>   (Interc…    15.8       9.27      1.71 9.78e-2
 2 Asia       1952 <tibble> <lm>   log(gdp…     4.16      1.25      3.33 2.28e-3
 3 Asia       1957 <tibble> <lm>   (Interc…    18.1       9.70      1.86 7.20e-2
 4 Asia       1957 <tibble> <lm>   log(gdp…     4.17      1.28      3.26 2.71e-3
 5 Asia       1962 <tibble> <lm>   (Interc…    16.6       9.52      1.74 9.11e-2
 6 Asia       1962 <tibble> <lm>   log(gdp…     4.59      1.24      3.72 7.94e-4
 7 Asia       1967 <tibble> <lm>   (Interc…    19.8       9.05      2.19 3.64e-2
 8 Asia       1967 <tibble> <lm>   log(gdp…     4.50      1.15      3.90 4.77e-4
 9 Asia       1972 <tibble> <lm>   (Interc…    21.9       8.14      2.69 1.13e-2
10 Asia       1972 <tibble> <lm>   log(gdp…     4.44      1.01      4.41 1.16e-4
# ℹ 110 more rows

Making a plot with error bars

lm_data <- gapminder |>
  nest(data = -c(continent, year)) |>
  mutate(
    fit = map(data, ~lm(lifeExp ~ log(gdpPercap), data = .x)),
    tidy_out = map(fit, tidy)
  ) |>
  unnest(cols = tidy_out) |>
  select(-fit, -data)

lm_data
# A tibble: 120 × 7
   continent  year term           estimate std.error statistic  p.value
   <fct>     <int> <chr>             <dbl>     <dbl>     <dbl>    <dbl>
 1 Asia       1952 (Intercept)       15.8       9.27      1.71 0.0978  
 2 Asia       1952 log(gdpPercap)     4.16      1.25      3.33 0.00228 
 3 Asia       1957 (Intercept)       18.1       9.70      1.86 0.0720  
 4 Asia       1957 log(gdpPercap)     4.17      1.28      3.26 0.00271 
 5 Asia       1962 (Intercept)       16.6       9.52      1.74 0.0911  
 6 Asia       1962 log(gdpPercap)     4.59      1.24      3.72 0.000794
 7 Asia       1967 (Intercept)       19.8       9.05      2.19 0.0364  
 8 Asia       1967 log(gdpPercap)     4.50      1.15      3.90 0.000477
 9 Asia       1972 (Intercept)       21.9       8.14      2.69 0.0113  
10 Asia       1972 log(gdpPercap)     4.44      1.01      4.41 0.000116
# ℹ 110 more rows

Making a plot with error bars

lm_data <- gapminder |>
  nest(data = -c(continent, year)) |>
  mutate(
    fit = map(data, ~lm(lifeExp ~ log(gdpPercap), data = .x)),
    tidy_out = map(fit, tidy)
  ) |>
  unnest(cols = tidy_out) |>
  select(-fit, -data) |>
  filter(term != "(Intercept)", continent != "Oceania")

lm_data
# A tibble: 48 × 7
   continent  year term           estimate std.error statistic       p.value
   <fct>     <int> <chr>             <dbl>     <dbl>     <dbl>         <dbl>
 1 Asia       1952 log(gdpPercap)     4.16     1.25       3.33 0.00228      
 2 Asia       1957 log(gdpPercap)     4.17     1.28       3.26 0.00271      
 3 Asia       1962 log(gdpPercap)     4.59     1.24       3.72 0.000794     
 4 Asia       1967 log(gdpPercap)     4.50     1.15       3.90 0.000477     
 5 Asia       1972 log(gdpPercap)     4.44     1.01       4.41 0.000116     
 6 Asia       1977 log(gdpPercap)     4.87     1.03       4.75 0.0000442    
 7 Asia       1982 log(gdpPercap)     4.78     0.852      5.61 0.00000377   
 8 Asia       1987 log(gdpPercap)     5.17     0.727      7.12 0.0000000531 
 9 Asia       1992 log(gdpPercap)     5.09     0.649      7.84 0.00000000760
10 Asia       1997 log(gdpPercap)     5.11     0.628      8.15 0.00000000335
# ℹ 38 more rows

Making a plot with error bars

ggplot(lm_data) +
  aes(
    x = year, y = estimate,
    ymin = estimate - 1.96*std.error,
    ymax = estimate + 1.96*std.error,
    color = continent
  ) +
  geom_pointrange(
    position = position_dodge(width = 1)
  ) +
  scale_x_continuous(
    breaks = unique(gapminder$year)
  ) + 
  theme(legend.position = "top")

 

Half-eyes, gradient intervals, etc

The ggdist package provides many different visualizations of uncertainty

library(ggdist)
library(distributional) # for dist_normal()

lm_data |>
  filter(year == 1952) |>
  mutate(
    continent = 
      fct_reorder(continent, estimate) 
  ) |>
  ggplot(aes(x = estimate, y = continent)) +
  stat_dist_halfeye(
    aes(dist = dist_normal(
      mu = estimate, sigma = std.error
    )),
    point_size = 4
  )

 

Half-eyes, gradient intervals, etc

The ggdist package provides many different visualizations of uncertainty

library(ggdist)
library(distributional) # for dist_normal()

lm_data |>
  filter(year == 1952) |>
  mutate(
    continent = 
      fct_reorder(continent, estimate) 
  ) |>
  ggplot(aes(x = estimate, y = continent)) +
  stat_dist_gradientinterval(
    aes(dist = dist_normal(
      mu = estimate, sigma = std.error
    )),
    point_size = 4,
    fill = "skyblue"
  )

 

Half-eyes, gradient intervals, etc

The ggdist package provides many different visualizations of uncertainty

library(ggdist)
library(distributional) # for dist_normal()

lm_data |>
  filter(year == 1952) |>
  mutate(
    continent = 
      fct_reorder(continent, estimate) 
  ) |>
  ggplot(aes(x = estimate, y = continent)) +
  stat_dist_dotsinterval(
    aes(dist = dist_normal(
      mu = estimate, sigma = std.error
    )),
    point_size = 4,
    fill = "skyblue",
    quantiles = 20
  )

 

Half-eyes, gradient intervals, etc

The ggdist package provides many different visualizations of uncertainty

library(ggdist)
library(distributional) # for dist_normal()

lm_data |>
  filter(year == 1952) |>
  mutate(
    continent = 
      fct_reorder(continent, estimate) 
  ) |>
  ggplot(aes(x = estimate, y = continent)) +
  stat_dist_dotsinterval(
    aes(dist = dist_normal(
      mu = estimate, sigma = std.error
    )),
    point_size = 4,
    fill = "skyblue",
    quantiles = 10
  )

 

Further reading